Published on

SHAP and Synergy

Authors

Understanding how and why a model produces an output is becoming an increasingly important stage when building a machine learning solution. Expanding on my explainability blogs this blog takes a brief look at Synergy, Redundancy and Independence which uses "sophisticated model inspection and model-based simulation to enable better explanations of supervised machine learning models."

Not only are data scientists required to produce an “accurate” and “reliable” model, we are also required to unravel our models:

  • Diagnostic: ensuring the model is not a victim to data leakage and has properly generalised to the training data.
  • Validation: check the plausibility of the relationships between the features and target variables.
  • Feature Selection: prune redundant features while keeping features that have “synergistic” features.
  • Fairness and compliance: avoid discrimination, bias, or other regulatory requirements. Yes, there are even GDPR requirements (some explanatory frameworks are achieving this compliancy).

Comparing coefficients of linear regression models, activations of neurons or tracking the number of times a feature is used within a random forest model still provides a limited insight into their decision making process.

SHAP

The most popular explanatory framework is Shapely Additive exPlanation (SHAP) but this also fails to unpack an arbitrary “black box” machine learning model. It uses local contributions of feature (or features) but is not designed for global relationships amongst features.

With SHAP we are not able to answer (the more challenging) questions about features:

  • Given a group of features, would there be less impact if their counterparts were absent?
  • Can features be substituted with little impact to the model performance?
  • What are the effects of a group of features on model performance?

Synergy, Redundancy and Independence

Given some features, we can take SHAP values and represent them as vectors. Following “decomposition”, we can split them into multiple subvectors. The driver for this is to capture information lost by Shapely values. By decomposing the values and given these subvectors, we can build three types of relationships for the features:

Synergy: given feature x1 relative to another feature x2 quantifies the degree to which predictive contributions of x1 rely on information from x2. For example, we can think of coordinates, longitude and latitude, would be related features and are used synergistically to predict - one cannot determine the outcome without the other.

Synergy is expressed as a percentage where 0% is full autonomy to 100% is full synergy and measures the global information of two interacting features contribute to the model predictions.

Redundancy: given two features x1 and x2, x2 might be redundant because x1 already contains the information present in x2. For example, height in inches and height in centimeters are highly redundant features.

Redundancy is expressed as a percentage where 0% is full uniqueness to 100% is full redundancy. The redundancy is asymmetric, one feature may be more redundant than the other. For example, house size and number of rooms. The number of rooms is more redundant than house size because house size can better compensate for the absence of number of rooms. Removing house size will be detrimental to the model performance.

Independence: features x1 and x2 are neither synergistic or redundant.

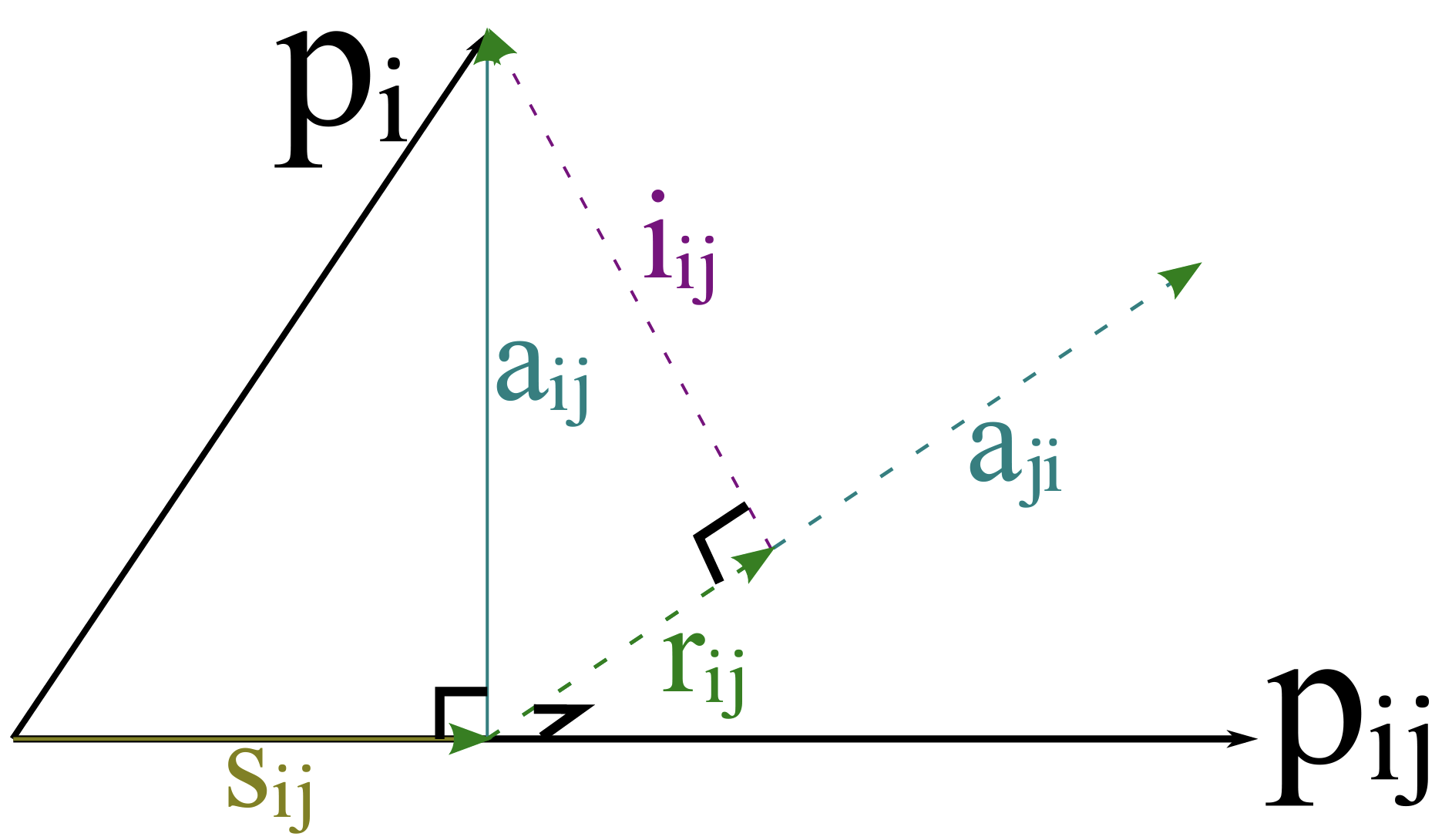
Geometric interpretation of synergy, redundancy and independence of feature xi relative to feature xj. The shap vectors are decomposed to produce S-R-I values.

All three of the relationships are expressed as percentages and features add up to 100%. Furthermore, feature relationships are not symmetrical meaning if feature x1 is synergistic with a group of others the reverse may not necessarily be true.

The details of SHAP and S-R-I is based on vectors and information provided within the vector space - for example, the vector angles between two vectors and decompose vectors into orthogonal components.

Conclusion

Model explainability is a growing area of research and will only become more important as machine learning models are used to make decisions. Frameworks like SHAP and LIME are locally comprehensive but still lack the global explanations that Synergy, Redundancy and Independence (S-R-I) decomposition of SHAP vectors offers. I am sure there will be new concepts to learn as this field grows, watch this space!

Further Reading: