This blog discusses the statistic tests that are commonly used by data scientists during various stages of machine learning workflows, carry out data analytics, and answer questions that can make better-informed business decisions. Statistics are used to study, manipulate, gather, analyze and draw conclusions from data. The two major areas of statistics are descriptive and inferential statistics.

Descriptive statistics is what you should have learnt during high school. It involves aggregated values of your data, such as the mode, mean, median, max, min, kurtosis, skewness, variance, standard deviation and inter quartile range. I won't go over each of them but a single Google search of each word should be self explanatory. Once you have done that come back here. All these values can be grouped into the larger groups: measure of central tendency, measure of variability, measure of frequency and measure of position.

Inferential statistics is used when you have a small sample of data and want to infer something about the larger population distribution. We perform data analysis on the sample and make generalizations about a population. This type of analysis can also be used to compare two or more groups of samples. We can do this by using the common methodologies: hypothesis tests, regression analysis and confidence intervals.

Inferential Statistics

Inferential statistics is, arguably, the most useful for day to day analysis. This blog provides an overview of the following inferential statistic methodologies:

• Hypothesis Testing
• ANOVA and T-Tests
• Correlation
  • Pearson correlation
  • Spearman correlation
  • Kendall correlation
• Contingency tables
• Chi Squared Tests
  • Test of Independence
  • Goodness of Fit
• Confidence Intervals
• Regression analysis

Hypothesis Tests

From hypothesis testing we gain an understanding about two mutually exclusive statements, about a population, to determine which statement is correct about the sample. Hypothesis testing consists of a null hypothesis that, typically, assumes there is no difference between the sample(s) and population; meanwhile, the alternative hypothesis is the opposite that assumes there is a statistical difference.

Before we dive deep into the type of methodologies, lets briefly run though Type I and Type II error. These type of errors are analogous to the terminology we use for classification problems.

Type I and II Error

*Type 1 Errors are false positives, where you reject the null hypothesis when it is actually true in the population. Meanwhile, Type II Errors are false negatives, where we fail to reject the null hypothesis when it is actually false in the population. See Paper on Hypothesis Testing and Error Types.

The probability of a Type I Error is called alpha, while the probability of a Type II Error is called Beta. Ideally, these value should be zero but this is very rarely the case in real world problems. One way to reduce these probabilities are to increase the sample size - as with all data science problems!

It is important to remember that we cannot completely eliminate these uncertainties and, when appropriate, should report the uncertainty whenever hypothesis testing. Another important point to remember is that we cannot ‘prove’ or ‘disprove’ anything by hypothesis testing and statistical tests.

To reject the null hypothesis, we must specify the maximum allowable probability of making a Type I Error, called the level of significance (denoted by alpha) for the test. Typically, this value is 5% or 1%, assuming a 95% or 99% confidence. When the p-value is less than the alpha value we can reject the null hypothesis and accept the alternative.

Another way to interpret the p-value is the probability that the observed difference occurred by random chance. So having p-value of less than 5% is what we want!

Hypothesis tests are used to provide a statistical comparison between each of the groups - sample or population. There are many tests we can perform, as highlighted below.

ANOVA Tests

Analysis of variance (ANOVA) tests are a collection of statistical models that are used to analyze the differences amongst an observed aggregated variability found inside a data set (i.e. means or medians). The number of independent variables determines whether you use a One-way or Two-way test.

The One-way ANOVA test is used to determine if there are any statistical difference between the means of three or more independent groups.

The Two-way ANOVA test is used when you have two independent variables that has been used to split the data. We then determine if there is a statistical difference and understand if there is an interaction between the two independent variables on the dependent variable.

ANOVA tests are similar to T-Tests but are used when you want to compare greater than 2 samples. For example, if you wanted to know whether the height of 3 school classes were statistically different based on their ages you would use a One-way ANOVA. Furthermore, if you would like to understand whether the age and gender played a role with the height we would use a Two-way ANOVA.

T-Tests

While ANOVA could be used to compare the height of 3 of more groups, we can use T-Tests to statistically compare two samples of data. For example, if we wanted to know whether 1 school class were taller than another we would use T-Tests.

However, what if we wanted to understand the relationship between the femur bone length and overall body height. Surely, these would be correlated.

Correlation Tests

Correlation tests allow us to understand the relationship between features. In ML it can help us understand the relationship between independent variables and the dependent variable. There are three frequently used tests.

1. Pearson correlation

Evaluates the linear relationship between two continuous variables. We would expect the femur bone length to be correlated with the overall body height - in face the ration is 4:1. The longer the femur the taller the person.

2. Spearman correlation

Evaluates the monotonic relationship. An example of this could be time spent exercising does not mean decreasing or increasing in body weight. The relationship can be defined as the value of independent variable increases, the value of dependent variable sometimes increases, but sometimes the value of dependent variable decreases.

3. Kendall correlation

Similar to Spearman where it evaluates monotonic relationships and measures the strength of dependence between two variables. This is the preferred correlation when there are small samples or some outliers.

Further reading on correlation:

• Differences between the correlation types
• Directory of Statistical Analyses

Contingency Tables

So far we have looked at statistical tests that can help us understand relationships between discrete and continuous numerical data. These methods cannot be used for categorical data, this is where contingency tables can be used.

The contingency tables are used in statistics to summarize the relationship between several categorical variables. This was first introduced by Karl Pearson, with the intent of being used to help determine whether one variable is contingent upon, or depends upon, the other variable. Contingency tables are used to compare the observed results to the expected results.

Chi Squared Tests

Chi Squared can be used to show the association between categorical variables. The greek symbol being χ2. Similar, to the other hypothesis testing statements, the Chi squared null hypothesis is no statistical difference whilst the alternative hypothesis shows that there is a statistical relationship. Generally, if the Chi squared contribution value is above the critical value for Chi squared then we can reject the null hypothesis, alternatively, if we are below then we accept the null hypothesis, i.e. there is no statistical difference between the categories within this dataset.

For example, on the table above we could use Chi Squared to statistical compare the categorical data and establish whether there is a significant relationship between the variables, i.e. favourite color and gender.

The benefit of Chi squared is the contribution plot that can be produced under a null hypothesis rejection. This analysis can be carried out as it is often useful to look at the cell-wise contributions of the χ2 statistic to see where the evidence for dependence is coming from. Pearson residuals can also be plotted in such a scenario and can also be used to quantify the difference between the observed in units of the dispersion of the fitted model.

A side note, that has not been covered in detail here, is the degrees of freedom within the dataset, a larger DoF affects the Chi squared distribution so ensure you take a look at that before performing the tests. Try to understand the Chi squared statistic formula if you want to learn more.

A small variation of Chi Squared is the G-Test. The Chi squared test gives approximately the same results as the G–test. However, unlike the Chi squared test, G-values are additive, which means they can be used for more elaborate statistical designs. More specifically, Pearson's Chi squared test is a score test, whereas the G-test is a likelihood ratio test. Researchers often conclude that the G-Test outperforms the Chi squared test. For most cases, you wouldn't expect to see a large difference between the two methods - speaking from experience, I tried all types of tests and resulted in the same conclusion. Nonetheless, while using Python, the G-Test can be performed by changing 1 input from SciPy.Stats power_divergence function (i.e. lambda_="log-likelihood").

There are many variations of Chi Squared tests but the two or the most popular that provides the insight required for most problems are:

1. Test of Independence

Tests whether there is a relationship between two types of categorical features, i.e. age groups and weather. Using the contingency table above, the chi squared test of independence can be used to establish whether the two variables are related. If the null hypothesis is rejected, then this implies the categorical data is related. For example, there are more males than females that prefer green as their favourite color.

2. Goodness of Fit

This type of Chi squared compares your sample of data against the population. It is used compare the distribution for a small sample vs the larger sample, i.e. compare the number of males and females that like green in a wider population. A very small Chi squared test statistic means there is a high correlation between the sample and population. Therefore, the sample data is a good fit for what would be expected in the general population. Alternatively, a large Chi squared value means the sample data does not fit the expected population data.

Overall, the Chi squared is extremely useful test to perform for categorical data, or numerical data that has been put into bins (e.g. age bounds 0-10, 11-20, 21-30 etc.).

Parametric and Non-Parametric Tests

All these tests might seem overwhelming at first but once you start running through a few examples it will start becoming very simple and logical. In fact, there are many flow diagrams, below, which allows you to figure out which methodology can be used to answer your question and fits the type of data. You don't need to memorize them but an overview of the parametric versions would be a great start.

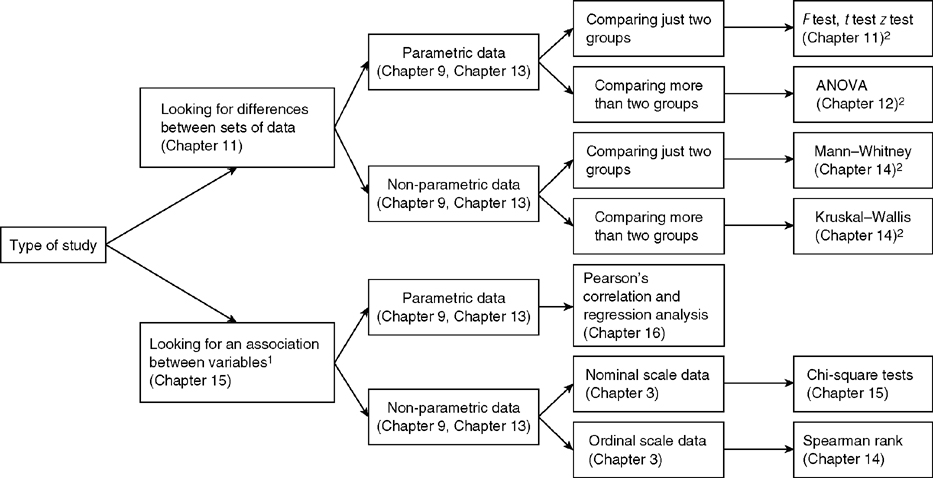
As you can see there are many methods in inferential statistics. However, there are several important considerations before we perform any type of test. This includes:

• Normality: does your data follow a normal (bell curve) distribution.
• Homoscedasticity: does your data follow variance within the data is constant.
• Is your data a representative sample from the population.
• Random independent samples.
• Comparable scale ratio level of measurement.
• No outliers.
• Homogeneity of variance.

In order to use a T-Test, it is assumed the Homogeneity of variance within the sample data is constant.

Fortunately, there are several alternative tests that we can perform instead of the standard test, these types do not have the same assumptions and are non-parametric alternatives. To perform these tests on Python we can use scipy.stats, read the guide here.

Parametric Tests are more powerful and are likely to detect a difference that truly exists with a lower chance of a Type 2 error, although, they do require a large sample size compared to Non-Parametric tests.

The specific Non-Parametric tests for each methodology have many underlining assumptions about the data, for example:

• Kruskal-Wallis and Friendman’s is an alternative for ANOVA tests and must have the same shape and equal variance.
• Man-Whitney test is an alternative for T-Tests but must have the same shape.
• Wilcoxon Signed-Rank Test is an alternative for a one-sample T-Tests but assumes that both populations must have symmetric distributions.

There are many other Non-Parametric tests, which have not been listed here, but have there own assumptions about the data being tested.

Conclusion

The concepts described above are commonly used by data scientists during various stages of machine learning workflows. The two major areas of statistics are descriptive and inferential statistics and will form the foundation in many day-to-day tasks in data science and are essential.

You do not need to remember all the tests highlighted within this blog but understanding the general logic behind how to approach a statistical problem is all you need. Even I have had to remind myself of the Chi squared logic many times and I am sure it will not be my last. There are many worked examples on the internet and on government websites, I recommend going through a few iterations of the methodology and writing null and alternative hypotheses to fully understand the concepts described.